
中学生向き通信教育「すらら」は偏差値どれくらい?については、総合的にいえば全教科60前後までの学習が可能というのが感想になります。また狙える志望校は標準~やや難関校クラスまで行けると思います。
さらに「すららの偏差値」について私たちの経験から詳しく解説をしていきます。
すららの教科から偏差値を見極めてみる
すららは中学生が最も苦手とする3教科(国語・英語・数学)の勉強ができますが、それぞれのカリキュラムから対応できる偏差値を考えてみようと思います。
その前に高校入試の過去問(2017年)から出題範囲を見てみるとこのようになります。
代表として東京都立高校の入試情報を参考にしています。
| 項目 | 内容 | 配点 |
| 漢字 | 書き取り・読みがな | 20 |
| 現代文の読解 | あさのあつこ「一年四組の窓から」 表現把握・理由説明・心情把握 | 25 |
| 論理・作文 | 原田信男「日本人はなにを食べてきたか」 作文200字・段落構成・内容把握・理由説明 | 30 |
| 古典 | 森澄雄・廣田二郎「芭蕉と現代」各務支考「芭蕉全集」 現代仮名遣い・内容把握・同意表現 | 25 |
ここから見えることは「内容把握」「理由説明」が主にウェイトを占めており、「作文」もそれと同じだけ重要な項目ということです。
100点満点中80点に絡んでいる項目なので、ここで点を取れることが重要です。
この出題で何割の点が取れるかが、大体の偏差値を見る基準になってきます。
過去3年間の出題を見ると、この4項目については毎年出題されています。
そろそろ別の項目もでてきそうな気はしますが、基本的にはこの4項目が主体となって出題されることは間違いないはずです。なのでここに重点を置いて勉強していくのもいいのではないかと思います。
すららの国語から偏差値を割り出す
まず3教科の中の「国語」から見ていこうと思います。
すららの体験口コミからわかった国語で勉強のできる単元はこのようになっています。
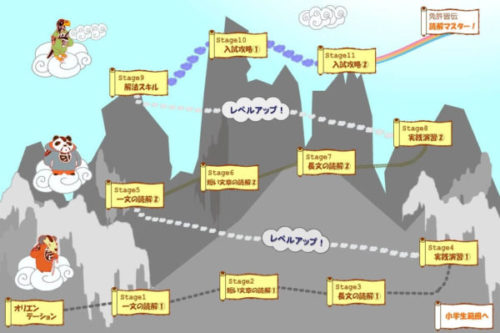

学校で習う順番に単元が並んでいますが、こうして見ると全ての単元をすららで体験できるのがわかります。まあこんなふうに全ての単元が勉強できるのは、当然と言えば当然なことです。
ただしそれぞれの単元をよく見てみると「読解」に関わっているものが多いんですね。
こうしてすららの体験口コミを見るとほぼ全てが読解に絡んでいることから、まずもって「高校入試のポイントをきちんと押さえている教材」といってもいいのではないでしょうか。
たとえばすららの映像授業Stage3「長文の読解」の内容を見てみると‥
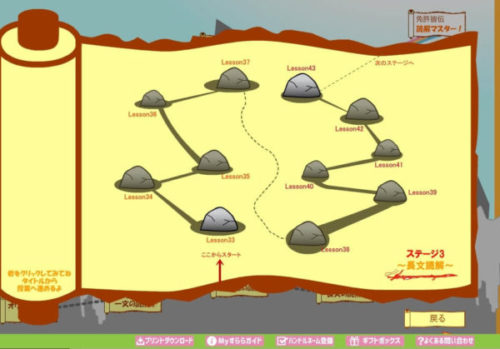
1つのStageだけで、11のレッスンからすららの体験口コミが成り立っています。
このようなStageがいくつかあるため、ボリュームとしては結構なものになります。
さらに、すららのレッスン内容は‥

このようなタイトルがついていますが、この時点で偏差値的には標準以上では‥といった予想がつくのではないかと思います。
論理構造と言われても、大人でも教養が伴っていなければ難しいはずです。
さらに具体的なすららの体験口コミについては‥
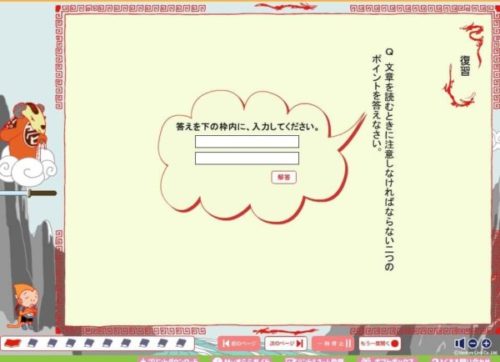
私も迷ってしまうような問題です。
初めの設問がこれなので、このあとのレベルは容易に想像がつくのではと思います。
初めに出される設問は、いわゆる「復習」になっています。

このようにそれぞれのStageで学習がリンクして繋がっているため、子供はスムーズにレベルアップしていけるのではないでしょうか。この辺りはすららが勉強になる、と本質で感じる部分ですね。
ちなみにこの問題の答えは「話題」「筆者の主張」になります。
そのあとの本題となる授業の様子はこうなります。

授業の中では、高校入試に関するポイントが説明される場面もあります。

こうして勉強ばかりではなく、時として高校入試を意識するように構成されているのもすららならではの特長でもあります。塾の講師を意識してシステムが作られたと聞いていますが、こういうアドバイスについての説明もある部分は講師を実感することができます。
このあとはその長文に対していくつかの設問があり、最後に復習へと続きます。

このすららの体験口コミを見て感じるのは、偏差値が標準よりも高めということです。
難関校でも対応できるでしょうし、もしかするとトップ校あたりに対応できると思われる設問も組み込まれています。
すららが中高一貫におすすめな3つの理由
そしてこの授業というのは、画面下のこの部分。

このノートで表示された授業の、1つに過ぎないんですね。

この授業が終わっても、また次のノートへ進んで授業が行われるという仕組みです。その授業でもまた、同じように復習から始まってその項の復習で終わるようになっています。
さらに授業を示すノートが進んで最後まで行くと‥

ここまで勉強してきた授業の、まとめプリントが始まります。
これは時間制限もないので、じっくりと取り組むことができます。
そしてさらにめとめプリントが終わると‥
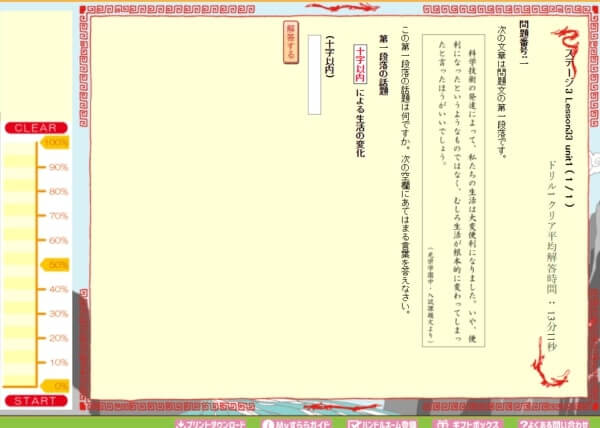
このようにドリルが始まって、ここでは時間の計測と正答率がチェックされます。
解答時間は全国平均のものに対して、自分のスピードチェックに役立ちます。

また正答率からは、スピードの速さだけが重要ではないことが理解できます。
速さと正確性を養うのに、我が家もかなり助かっている役に立つドリルです。
このようにすららの国語を見てみると、高めな偏差値に対応できることが分かります。
もちろん基礎から学べますので、標準校狙いであっても勉強になります。

トップ校となるとさすがに難しいかと思いますが、単元をすべて学べるすららの体験口コミをベースにしながら参考書などを併用すれば狙えないこともないのかな?という感じがします。
すららの英語から偏差値を割り出す
すららの体験口コミで勉強できる3教科の中から、英語について詳しく見ていきます。
やはり基準となるものとして、東京都立高校の入試過去問から探ってみようと思います。
2017年に出題された、東京都立高校における入試問題の内訳です。
| 項目 | 内容 | 配点 |
| リスニング | 対話文・英文と質問 | 20 |
| 会話文 | 適語選択・内容把握・具体的な内容選択・理由選択 | 24 |
| 長文読解 | 適語選択・内容一致文選択・適語補充・作文 | 28 |
| 長文総合 | 文整序・内容把握・英問英答選択 | 28 |
ここでのポイントは、おもに「長文の読解」がウェイトを占めています。
長文に関する項目だけでも、28点×2項目=56点と半分以上のポイントとなります。
しかし8割のウェイトを占める長文は、そんなわけにもいきませんね。
過去3年の入試問題を見ても、まったくこの通りのウェイトになっています。

さらに新学習指導要領ではとくに英会話が強化されますので、この長文読解はこれ以上ないほどに勉強しておいて損はありません。
というわけで、すららの英語では「長文読解」にポイントを置いて偏差値を探っていきます。
まずすららの英語で学べる単元についてです。
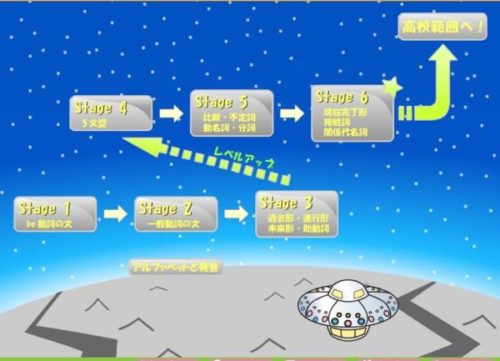
これが全ての単元ですが、一見すると少ないように見えます。
しかし決してそうではなく、Stageごとでさらに細かくレッスンが用意されています。
Stage1「be動詞の文」を見ていきます。
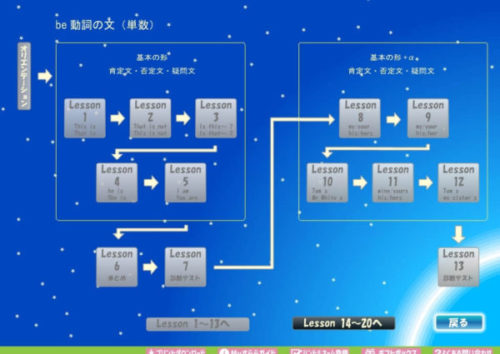
このレッスン1~13までが、単数についてのカリキュラムとなっています。
複数についてのカリキュラムは‥
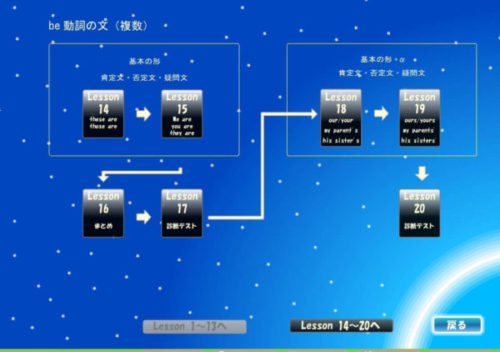
レッスン14~20での構成となっており、最後は診断テストで終わります。
このようにStageひとつを取ってみても、すららの体験口コミのレッスン数のボリュームはかなり膨大なものです。
ではStage1「be動詞の文」でも後半の、レッスン8の内容を詳しく見ていきます。
レッスンを選ぶと、このようにさらにUnitとして細かく分かれています。
Stage ➝ Lesson ➝ Unit
3教科の中でも英語については、とくにボリュームが多いことがわかります。
少し進んでUnit34を見ていきます。

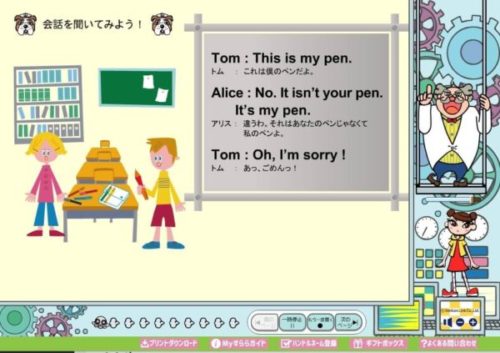
すでに最初のStage1からそうなのですが、授業は基本的にヒアリングベースで行われます。
講師の説明は日本語ですが、設問などは英会話で進んでいきます。
英会話を聞き取って、さらに文法などの設問に答えるといった形式です。

まだこの時点では短めの文章となっており、単語の使い方について基本的な勉強ができるといった要素のほうが大きいです。
いちばん最後のほうのStage6に進んで見ていきます。

この辺りになってくると、英語学習の終盤ということで長文の読解が基本です。
授業の様子はこのような感じです。
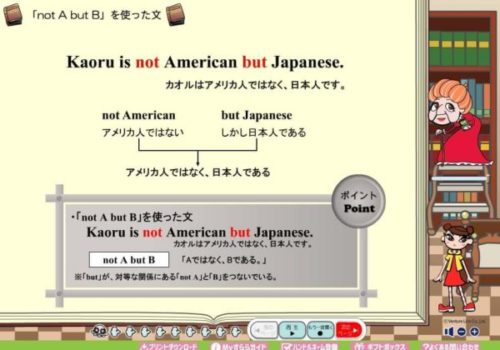
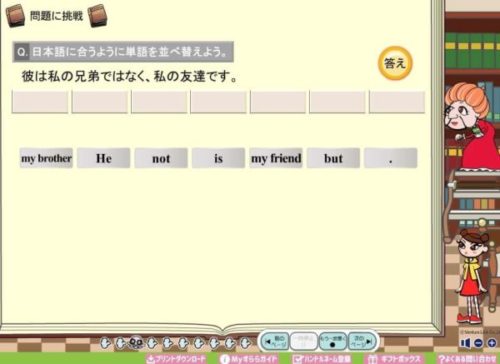
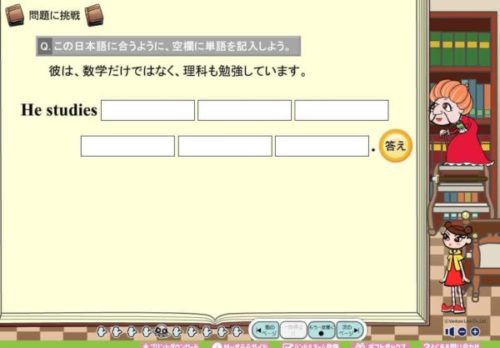
文法を理解した上、単語も覚えていないと解けない問題ばかりが出されます。
この辺りの出題のされ方は英検のスタディギアと似ていますが、すららは授業での説明があるだけにより理解しやすいかもしれません。
英検でいうところの4~3級といった内容でしょうか?
少し内容が優しいように思いますが、これが学校の授業での範囲です。
英検を受験していると戸惑うところがありますが、いかに学校で習った範囲を的確に答えるかが高校入試では大事です。すららの授業は学校で習い範囲を的確に捉えている、そんな授業であることがわかります。
一通りの授業が終わったら、速さと正確性を養うドリルが行われます。
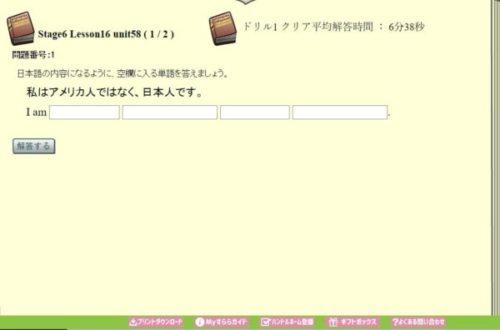
語句の並び替えもありますが、設問の多くは直接単語を入力するというものです。
スペルもしっかりと覚えておかなければ、問題を解くことはできません。
さらにネイティブが実際の声を担当しているため、正しい発音を身につけることができます。

偏差値的には中学生で習う範囲は網羅していますが、すららは直球での学習には強いのですが変化が施してある問題には対応しきれないのかもしれません。
そのため難関校までは偏差値の範囲としても、トップ校となれば難しいのかなと思います。
変化のある問題がどれだけ出題されるかはわかりませんが、どこまで拾っていくか?といった戦略的なことも踏まえて考えると、すららの英語体験はもう少しハイレベルな学習にも対応できると考えます。
すららの数学から偏差値を割り出す
すらら3教科のうち、数学の偏差値について探っていきます。
ここでも同じように、東京都立高校の過去問をベースに考えてみます。
| 項目 | 内容 | 配点 |
| 小問 | 小数・分数・平方根・一次方程式・連立方程式・二次方程式・二次関数・確率・二等分線の作図 | 46 |
| 数列や規則性 | 規則性・証明 | 12 |
| 一次関数のグラフ | 面積・面積比 | 15 |
| 平面図形 | 弧の長さ・線分比・相似の証明 | 17 |
| 空間図形 | 線分の長さ・立体の体積 | 10 |
全体的に広く出題されていますが、その中でも「図形」に関する項目が目立ちます。
平面・空間図形はもちろんこのと、そのほかの項目でも図形が関わっているのがお分かりいただけるでしょうか?
面積なども図形を理解していることが基本となりますし、作図などもそうですね。

考える角度は異なるとしても、基本となるのは図形についての理解度です。図形を押さえておくことで、約半分ほどはポイントを得ることができるはずです。
過去3年間の問題を見ても、図形分野からの出題が最も多くなっています。
このことから、すららの数学では図形に焦点を当てて探っていきます。
すららで学習の出来る内容はつぎの通りです。
すららの数学ではやはり広く全般的に学習ができるようになっていますが、とくにポイントとなる図形分野についても結構なボリュームがあります。
図形の最初のStage「平面図形(1)」について見ていきます。
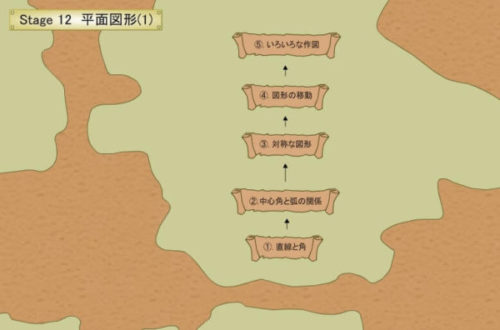
「平面図形(1)」を選ぶと、さらにこのようにカリキュラムが細かく分かれています。
いちばん最初の「①直線と角」を選んでみます。
すららの授業は得てして理解しやすいのですが、この図形でも学校では教わらないような言葉を使って感覚で理解できるようになっているのが特長です。

すららの体験口コミ授業が一通り終わると、このようにまとめプリントに記入して身につけるような工夫が施されています。いわゆるノートまとめと復習が一度にできる、といった感覚のプリントです。
さらに授業の合間には問題定義がなされるため、少しずつ理解できるのではないでしょうか。
もうひとつ気になるのが空間図形ですが、ひとつすららの体験口コミから参考までに見てみます。
空間図形でいちばん理解に苦しむのは、いったいどの部分かご存知でしょうか?

私も学校の先生に伺ったことがあるのですが、3次元特有の「奥行き」の感覚を掴む部分が最も理解に時間がかかるとのことでした。
そこで「空間図形の奥行き」をいかに理解できるか?という部分にポイントを置きながら、すららの空間図形の授業を探ってみようと思います。
空間図形で奥行きを理解するためには、立体図形を理解していることが先になります。
すららの授業で見ると、このように理解を促しています。
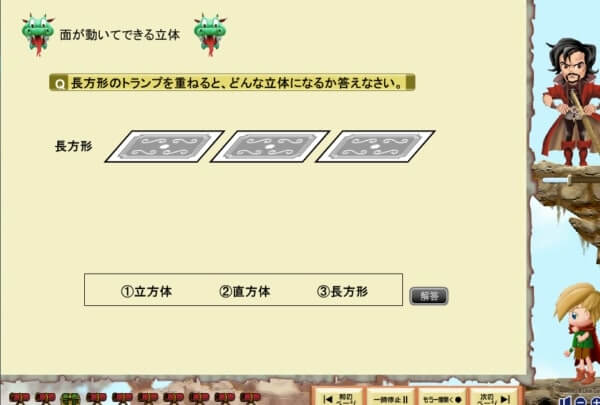
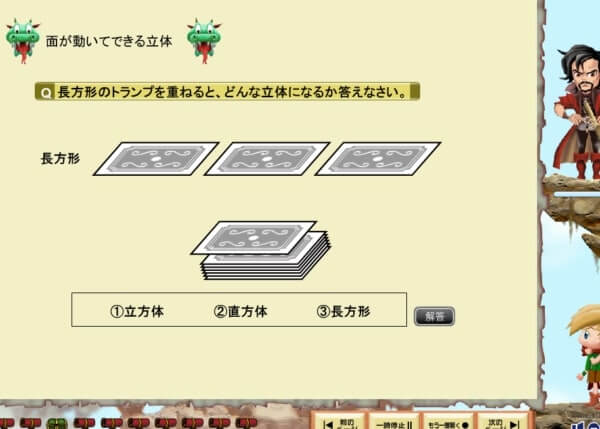
ここでは画像なのでお伝えしきれませんが、トランプが動いて積み上がることによって理解を促しています。つまり紙で見るのとは違って、動画ならではの「動き」によってより理解に近づけることができるというものです。
実際に動きがあることで、図形の理屈、とくに「奥行き」について感覚で理解することができるというのがすららの授業です。
もうひとつ例を挙げて授業を見てみます。
この授業は平面図形からどんな立体ができるか?という問題ですが‥
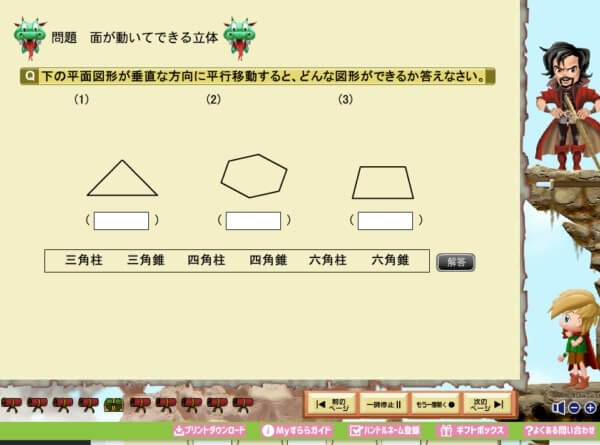
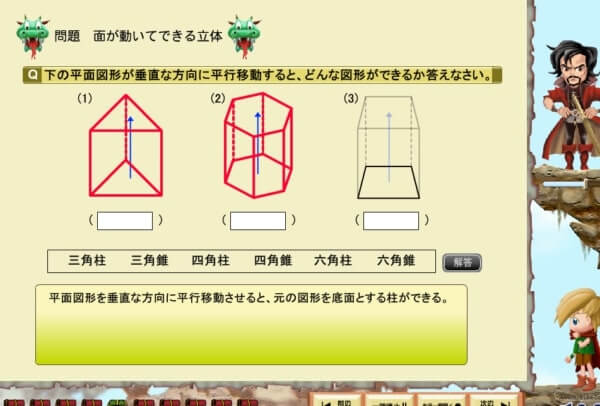
このように動画ならではの動きによって、理屈が理解しやすくなります。

とくに空間図形のように奥行きの理屈を身につけるためには、このような「感覚」で立体を感じるといったほうが理屈がわかりやすいのかもしれません。
すららの数学では、広い分野について予習と復習を用いながら学習できることは他の教科と同じですが、とくに高校入試のポイントにもなる「図形」の理屈について感覚を通して理解できる部分が優れているのではと感じます。
ここでは他分野についてはお伝えしきれませんでしたが、偏差値的には難関校クラスまでは十分に狙える内容だと思います。
しかしそれ以上に、まず数学の入り口ともいえる「感覚で第一歩の踏み出し方がわかるようになる」という部分については、私は特筆すべきすららの体験口コミ授業内容ではないかといった感想を持ちます。
またスマートプロケッターという機能もあるので広く数学に対応できます。
さらに詳しい内容については、すらら公式サイトのほうがわかりやすいと思います。

すららの偏差値から考えるコース設定

すららは教科以外にもコースが設けられており、偏差値を考える上でプラスアルファの効果を持っていると思われます。
「中学英語総復習コース」

すららの英語授業とは別に、高校入試前の総まとめとともに偏差値の確認にも役立つコースとなっています。
うまく利用すれば志望校に対して、偏差値的にもやや有利に働くのではといった期待を持っています。
「英検対策コース」
5級~2級まで対応しているため、中学生の間に習得させたい3級は十分に対応しており、カリキュラムも3級対策で28時間といったボリュームということで英検クリアに向けて役立つコースとなるはずです。
高校入試には直接関係はありませんが、英検を学習することによって本来の英語力を持ち上げる働きを期待できるため、偏差値の向上にも関わることは間違いないのではと思います。
「数学検定対策コース」
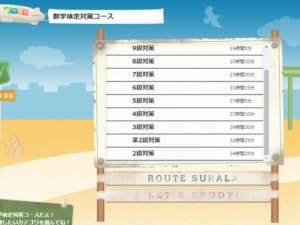
英検と同じような扱いができますが、計算スピードの向上、正答率の向上などにプラスになることによって、本来の数学の偏差値の底上げが期待できる検定です。
もし検定を受けなかったとしても、子供の数学力をより確かなものにすることのできるコースではないかと期待しています。
「SPI対策コース」

というのは最近とくに注目を集めている能力判定方法で、これから社会人になる子供にとって必ず役立つ能力と思っています。
とくに就職時においては都会の企業を筆頭に、このSPI試験が行われることが多くなりつつあります。今後は間違いなく判断基準として利用される可能性が、限りなく高い能力です。
直接的に偏差値とは関係がありませんが、理屈の考え方向上につながることで勉強にも影響を与えるものになるのではないでしょうか。
まとめ

このようなことから、すららの体験口コミを総合的に考えると偏差値は難関校までに対応しているのではといった見方がかなり強いです。難関私立高校のトップ校となると少し物足りないような気がします。
私の結論としては、すららの対抗できる偏差値はこのようになります。
- 標準校~難関校までに対応できる
- 偏差値60までであれば十分に対応が期待できる
- 難関私立高校の難問対策までは難しい
難関私立高校の受験対策になると、すららをベースとして、ほかに何かひと工夫ほしい所です。
もし中学生の子供へすららをお考えであれば、トータルで見ると授業のわかりやすさが極めて光るすららの体験口コミだというのが感想です。
次世代対話型アニメーション授業という肩書がついていますが、その名前の通りこれからの時代を担っていくのにふさわしいアダプティブラーニング教材がすららではないでしょうか。
すららの無料体験で偏差値をチェックしてみてください。

我が家のすらら体験談



コメント